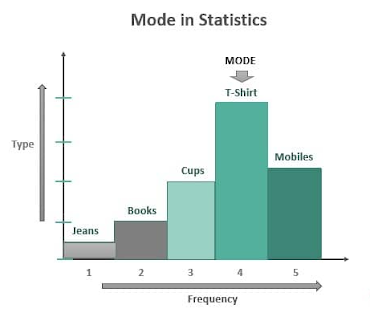
Mode example (Grouped data)
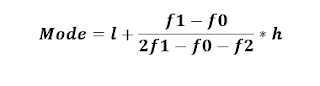
Below given is the data representing the scores of the students in a particular exam. Let us try to find the mode for this: Exam Score (x i ) (f i ) 41-50 2 51-60 9 61-70 7 71-80 15 81-90 6 90-100 3 Modal class = 71 - 80 (This is the class with the highest frequency). The Lower limit of the modal class (l) = 71, Frequency of the modal class (f1) = 15, Frequency of the preceding modal class (f0) = 7, Frequency of the next modal class (f2) = 6, and Size of the class interval (h) = 10. Thus, the mode can be found by substituting the above values in the mode formula, Therefore, the mode for the above dataset is 75.71.